
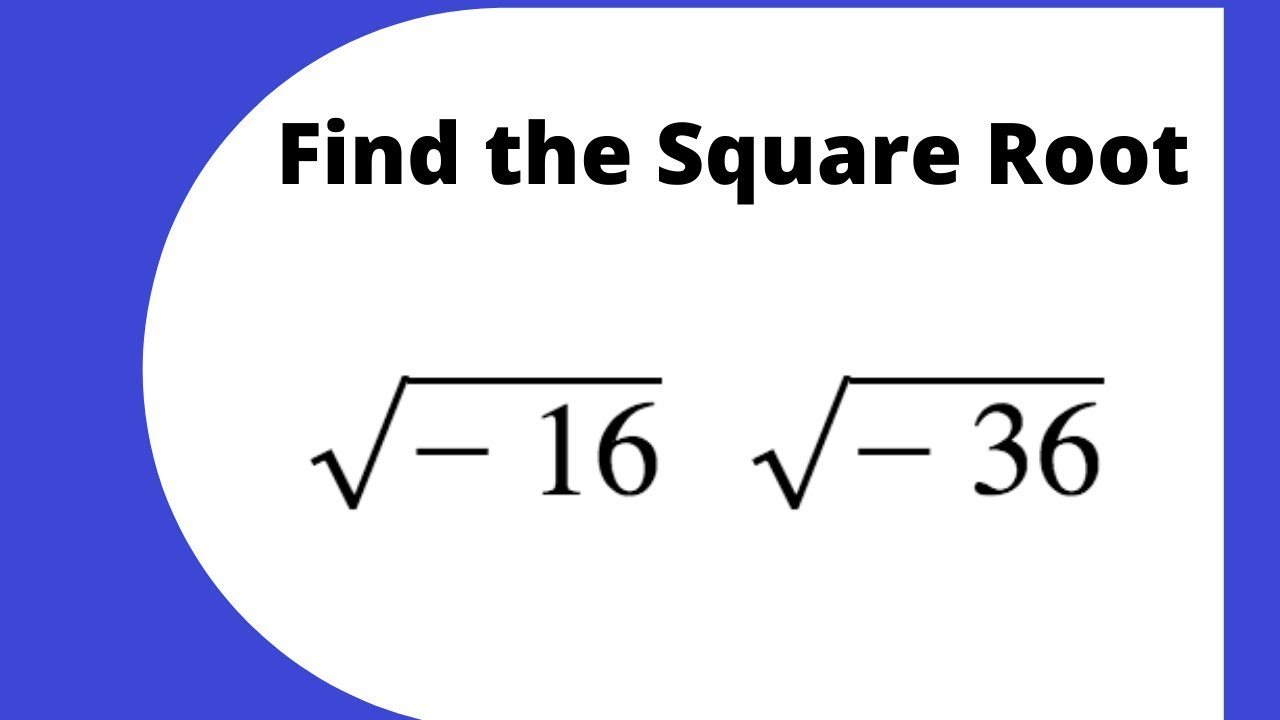
Using a valuable equation from geometry, the Pythagorean theorem, we know that a² + b² = c², where a and b are the legs of the right triangle and c is the hypotenuse. So, essentially, this boils down to solving for the hypotenuse of a right triangle: You can determine from regulation tennis court dimensions that the baseline is 27 feet long, and the sideline (on one side of the net) is 39 feet long. This is because to square a number just means to. Any nonnegative real number x has a unique nonnegative square root r this is called the principal square root.

For example, the square roots of 9 are -3 and +3, since (-3) 2 (+3) 2 9. Since a positive number multiplied by itself (a positive number) is always positive, and a negative number multiplied by itself (a negative number) is always. 'Note that any positive real number has two square roots, one positive and one negative. Square roots is a specialized form of our common roots calculator. How far must Nadal run to reach the ball? In fact, any number at all can be squared, even numbers like pi and 0. Given a number x, the square root of x is a number a such that a2 x. Now, assume his opponent has countered with a drop shot (one that would place the ball short with little forward momentum) to the opposite corner, where the other sideline meets the net: We assume that any radicand is a result of elementary mathematical operation multiplication of two real numbers b x b z, positive, negative and their mix, e.g. Imagine that Rafael Nadal, one of the fastest players in the world, has just hit a forehand from the back corner, where the baseline meets the sideline of the tennis court: We don't need complex numbers (imaginary number i) to calculate the square roots of negative numbers. To see a real-world application of the Python square root function, let’s turn to the sport of tennis. In mathematics the symbol for (1) is i for. Technically there is not a square root for negative numbers.

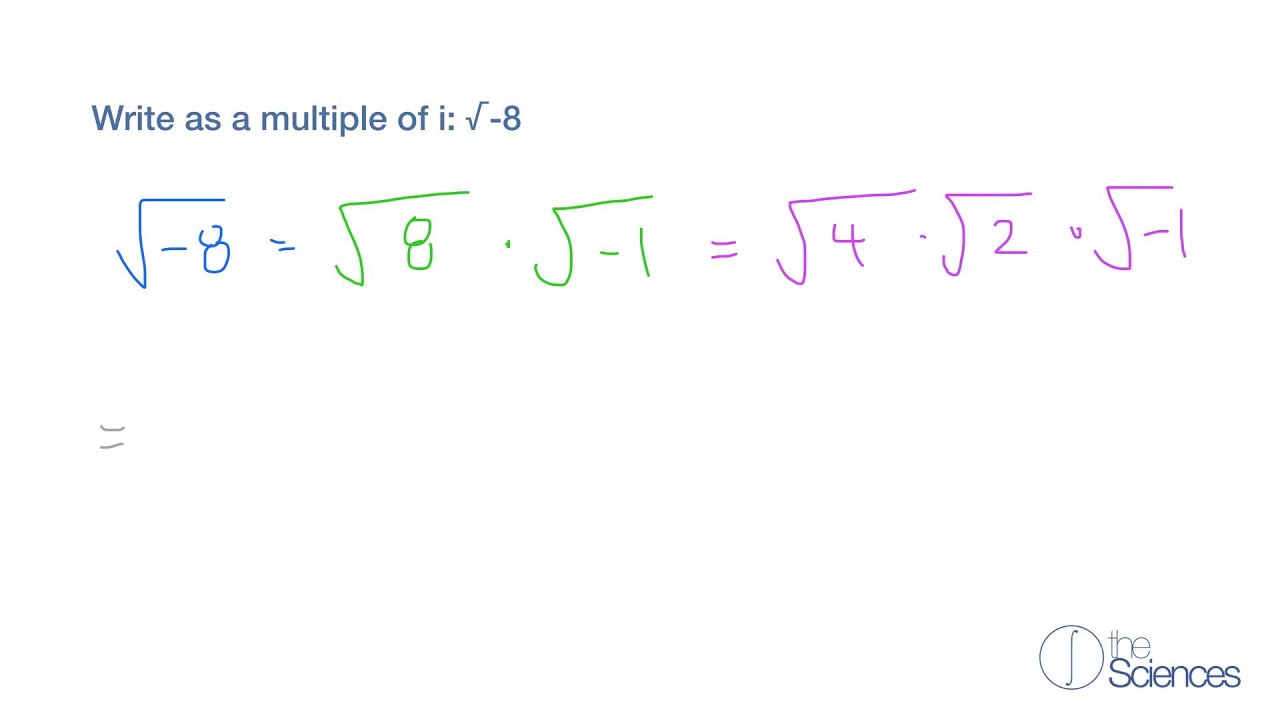
For example there is no real square root of -9, because -3 × -3 +9, and +3 × +3 +9 also. In this video, I find the square root of negative numbers. There are no real even-order roots of negative numbers. Instead, the square root of a negative number would need to be complex, which is outside the scope of the Python square root function. The square root of minus one (1) is the unit Imaginary Number, the equivalent of 1 for Real Numbers. Find the square root of negative numbers. If you attempt to pass a negative number to sqrt(), then you’ll get a ValueError because negative numbers are not in the domain of possible real squares. While Girolamo Cardano was working on solving cubic and quadratic equations in 1539, he encountered some formulas that involved square roots of negative numbers. sqrt ( - 25 ) Traceback (most recent call last):įile "", line 1, in ValueError: math domain error Apparently it depends on the region of the complex plane you choose your initial guess from, whether it will/won't converge to a root/the root you're looking for.> math. There's also examples (which I'd link but I'm restricted to only two links) of functions for which Newton's Method cycles and for which it diverges for given initial conditions, which have real roots.Īnyway if you wanted you could look up Newton's fractal it has some info for sequences converging to complex roots. SQRTPI : Returns the positive square root of the. Often one will abbreviate "the square root function applied to $x$" or equivalently "the positive square root of $x$" as simply "the square root of $x$," if no confusion should arise. To find the negative root of value, simply multiply the result of the SQRT function call by -1. However for positive reals $x$, by definition the square root function applied to $x$ yields the positive square root. Thus, both $+7$ and $-7$ are square roots of $49$. We say $x$ is a "square root" of $y$ if $x^2=y$. It has since been deleted, but here is my answer to that other question, which is also pertinent here. Also clear, I think, is that whether or not a person uses imaginary. JChau asked in a separate question if it's ever possible for the square root of a number to be negative, and another user moved for that to be closed as a duplicate of this one. However, it is clear that imaginary numbers are useful to some people, but not to others.


 0 kommentar(er)
0 kommentar(er)
